💡 시간복잡도
서로 다른 알고리즘의 효율성을 비교할 때 사용
시간복잡도 효율순 : O(1) < O( 𝑙𝑜𝑔𝑛 ) < O(n) < O(n 𝑙𝑜𝑔𝑛 ) < O( 𝑛2 ) < O( 2𝑛 ) < O(n!)
Big O 표기법이란?
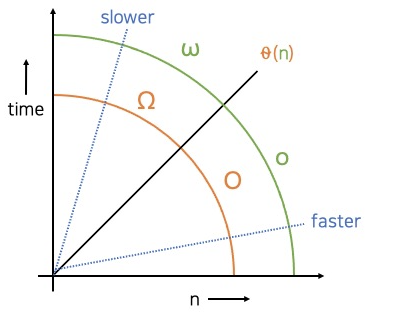
- O (빅 오 복잡도) : 비교 대상인 그래프가 일치 혹은 아래에 있을 때. 비교 대상인 다른 알고리즘과 같거나 더 빠르다.
- θ (세타 복잡도) : 비교 대상인 그래프가 일치할 때. 비교 대상인 다른 알고리즘과 같다.
- Ω (빅 오메가 복잡도) : 비교 대상인 그래프가 일치 혹은 위에 있을 때. 비교 대상인 다른 알고리즘과 같거나 느리다.
- o (리틀 오 복잡도) : 비교 대상인 그래프가 아래에 있을 때. 비교 대상인 다른 알고리즘보다 더 빠르다.
- ω (리틀 오메가 복잡도) : 비교 대상인 그래프가 위에 있을 때. 비교 대상인 다른 알고리즘과 느리다.
부등호로 Big O 표현
O (빅 오 복잡도) : <=
θ (세타 복잡도) : =
Ω (빅 오메가 복잡도) : >=
o (리틀 오 복잡도) : <
ω (리틀 오메가 복잡도) : >
시간복잡도의 규칙
- 규칙 1
- input(입력값)은 항상 0 보다 크다
- 음의 입력값은 시간복잡도를 고려할때 말이 되지 않는 경우임
- 규칙 2
- 컴퓨터 과학의 관점에서 함수는 많은 입력값이 있을때 더 많은 작업을 하게 됨
- 규칙 3
- 시간복잡도에서는 모든 상수를 삭제함 (ex: 3n = n, 5n = n)
- 규칙 4
- 낮은 차수의 항은 무시한다
- n과 n^2 를 비교할때 그래프에서 (1,1)인 지점까지는 n이 더 오래걸릴 수 있지만
알고리즘에서는 입력값이 1 보다 작은 값은 고려하지 않기 때문에
n이 무한으로 커진 경우를 가정하고 비교를 해야함 - n^3 + n^2 + n 이라는 함수가 있을때, n^2과 n은 알고리즘의 시간복잡도에 영향을 미치지 않고,
n^3 만이 입력값이 무한이 될때 고려해야할 부분이다
- 규칙 5
- 시간복잡도 함수가 log 함수를 포함할 경우 밑은 무시한다
- 모든 로그는 서로 배수 관계이므로, 복잡도에 관해선 로그의 밑을 고려하지 않아도 됨
- 복잡도가 log인 알고리즘은 보통 무언가를 반으로 나누거나 2를 곱한 경우 자주 사용 됨
ex: 반복문에서 무언가를 탐색하면서 반으로 나누거나 2를 곱할때 복잡도는 밑이 2인 로그가 됨,
10으로 나누거나 10을 곱하면 밑이 10인 로그가 되고,
이때 밑은 무시하고 log(n)의 시간복잡도를 가진다고 표현함
- 규칙 6
- 등호를 사용하여 표현한다
- ex: 2n = O(n) -> 2n은 O(n)이라는 함수의 집합에 속함
시간복잡도가 O(1) 인 경우
- O(1)은 constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않음.
- 입력값의 크기와 관계없이 즉시 출력값을 얻어낼 수 있다는 의미임
- 예를들어 arr의 길이가 100만이라고 해도, 즉시 해당 index에 접근해 값 반환 가능
- 규칙 1
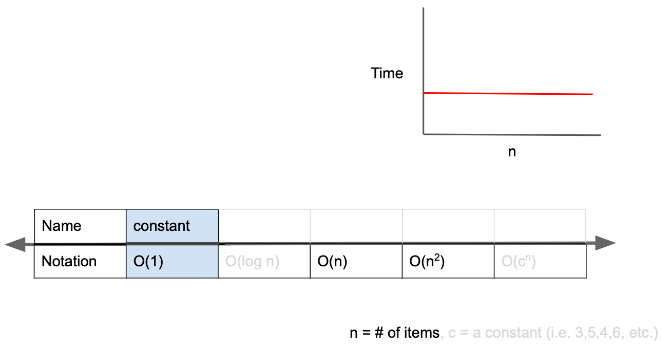

입력값의 크기가 아무리 커져도 즉시 출력값을 얻어낼 수 있는 O(1) 알고리즘 예시
시간복잡도가 O(n) 인 경우
- linear complexity라고 하며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가함
- 예를들어 입력값이 1일때 1초의 시간이 걸리고,
입력값을 100배 증가시켰을때 100초가 걸리는 알고리즘을 구현했다면,
그 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있음.
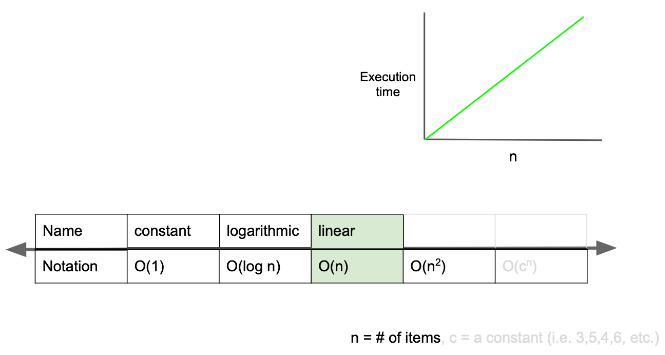
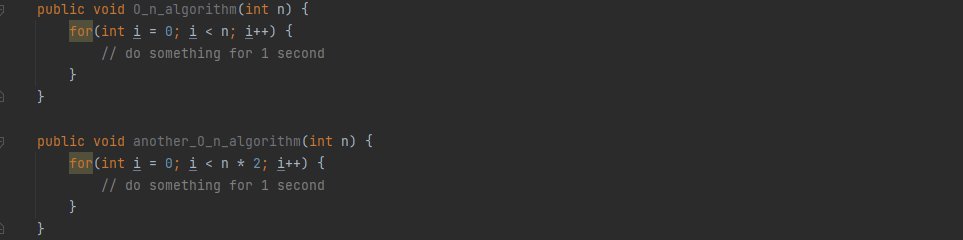
첫번째 함수에선 입력값(n)이 1 증가할때마다 코드 실행시간이 1초씩 증가함
두번째 함수는 입력값이 1 증가할때마다 코드 실행시간이 2초씩 증가하므로 이 알고리즘은 O(2n) 이라고 표현할 수 있음
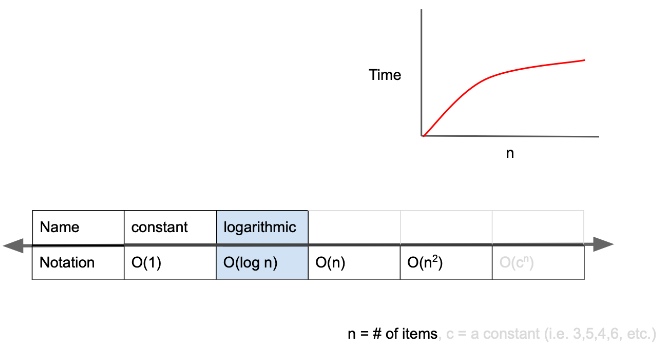
시간복잡도가 O(log n) 인 경우
- logarithmic complexity라고 하며, Big-O 표기법중 O(1) 다음으로 빠른 시간복잡도를 가진다
- 자료구조에서 배웠던 BST에선 원하는 값을 탐색할때, 노드를 이동할때마다 경우의 수가 절반으로 계속 줄어듬.
BST의 값 탐색과 같은 로직으로 O(log n)의 시간복잡도를 가진 알고리즘(탐색기법) 임
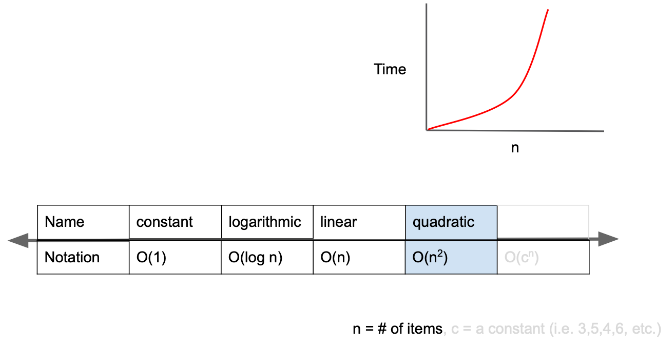
시간복잡도가 O(n^2) 일 경우
- quadratic complexity라고 하며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가
- 예를들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주니 25초가 걸리게 된다면
이 알고리즘의 시간복잡도는 O(n^2)라고 표현함
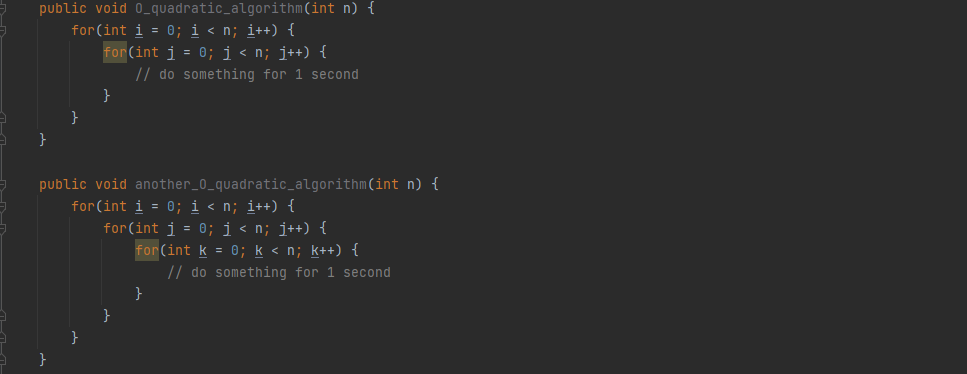
2n, 5n을 모두 O(n)이라고 표현하는 것 처럼, n^3과 n^5도 모두 O((n^2)로 표기함. n이 커질수록 지수가 주는 영향력이 점점 퇴색됨
시간복잡도가 O(2^n) 일 경우
- exponential complexity라고 하며, Big-O표기법 중 가장 느린 시간복잡도를 가짐
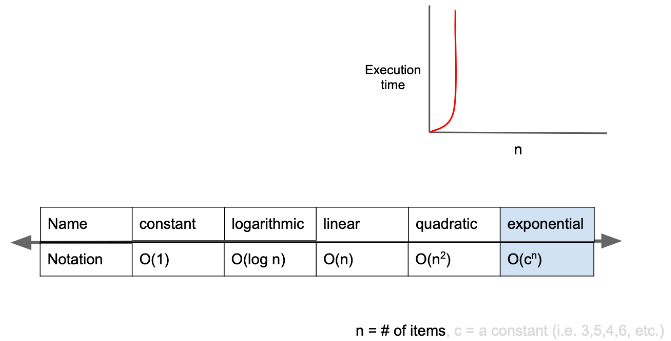

재귀로 구현한 fibonazzi 수열은 O(2^n)의 시간 복잡도를 가진 대표적인 알고리즘임.
'📚 Data Architect > Data Structure' 카테고리의 다른 글
| Stack (0) | 2023.04.13 |
|---|---|
| Doubly Linked List & Circular Linked List (0) | 2023.04.13 |
| Singly Linked List (단순 연결 리스트) (0) | 2023.04.13 |
| Iterator (0) | 2023.04.13 |
| 자료구조 기본 개념 (0) | 2023.04.13 |